Matemáticas: Fibonacci

Me resulta inevitable publicar de vez en cuando algún tema relacionado con esa disciplina que estudié y que forma parte inextricablemente de nuestras vidas, lo queramos o no. En esta ocasión, quiero mostraros que las matemáticas no son sólo números (o letras, según se mire), derivadas e integrales, sino que hay detrás un montón de historias y anécdotas que pueden resultar interesantes.

Empezaremos mencionando a un afamado pisano que seguro conocéis, pues debe de ser de los matemáticos más veces citados en novelas. Se trata del también conocido como Fibonacci ("hijo de Bonaccio"), uno de los grandes matemáticos europeos de la Edad Media sino el más importante.

Leonardo de Pisa -éste era su nombre- nació en 1170 y falleció en 1241. Se aficionó a las matemáticas siendo un chiquillo, tras un curso de aritmética posicional hindú que su padre, director de la oficina de aduanas en una factoría mercantil italiana asentada en Bougie, Argelia, le hizo seguir. La más conocida de sus obras, Liber abaci (1202) (literalmente, Libro del ábaco) era en realidad un amplio tratado del sistema de numeración indoarábigo, en el que presenta los signos hindúes y el 0 (quod arabice zephirum appellatur), y el método de regula falsi para ecuaciones de primer grado. Sin embargo, sus razonamientos no parecieron causar demasiada impresión a los mercaderes italianos de la época. Aunque, con el tiempo, su libro llegaría a ser la obra de máxima influencia entre todas las que contribuyeron a introducir en Occidente la notación indo-arábiga.

En De quadratis numeris (hacia 1225), que se perdió y apareció en 1853 en la Biblioteca Ambrosiana de Milán, cuando muchos pensaban que sus resultados estaban copiados de Diofanto, supera a éste y a los árabes y sólo es superado por Pierre Fermat en el siglo XVII.

No deja de ser irónico que Leonardo, cuyas aportaciones a la matemática fueron de tanta importancia, sea hoy conocido sobre todo a causa de un matemático francés del siglo XIX, Edouard Lucas, interesado por la teoría de números (y recopilador de una clásica obra de matemáticas recreativas, en cuatro volúmenes), quien encadenó el nombre de Fibonacci a una sucesión numérica que forma parte de un problema trivial del Liber abaci. La sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 11...), en la que cada término es la suma de los dos anteriores (Fn=Fn-1+Fn-2, ha tenido intrigados a los matemáticos durante siglos, en parte a causa de su tendencia a presentarse en los lugares más inopinados, pero sobre todo, porque el más novel de los iniciados en teoría de números, aunque sus conocimientos no vayan mucho más allá de la aritmética elemental, puede aspirar a investigarla y descubrir curiosos teoremas inéditos, de los que parece haber variedad inagotable. El interés por estas sucesiones ha sido avivado por los desarrollos en programación informática, ya que al parecer tiene aplicación en clasificación de datos, recuperación de informaciones y generación de números aleatorios.

Seguramente la propiedad más notable de la sucesión de Fibonacci sea que la razón entre cada par de números consecutivos va oscilando por encima y debajo de la razón áurea, y que conforme se va avanzando en la sucesión, la diferencia con ésta va haciéndose cada vez menor; las razones de términos consecutivos tienen por límite, en el infinito, la razón áurea. La razón áurea es un famoso número irracional (pero no trascendente como Pi, que no tiene representación algebraica), de valor aproximado 1,61803..., que resulta de hallar la suma de 1 y la raíz cuadrada de 5, todo dividido por dos.

Estatua de Leonardo en el Campo Santo de Pisa (1863)

Profundizando más sobre la sucesión de Fibonacci
Hay abundante literatura dedicada a la aparición de la razón áurea y de la sucesión de Fibonacci tan relacionada con ella, en el crecimiento de los organismos y a sus aplicaciones a las artes plásticas, a la arquitectura e incluso a la poesía. George Eckel Duckworth, profesor de clásicas en la Universidad de Princeton, sostiene en su libro Structural Patterns and Proportions in Vergil's Aeneid (University of Michigan Press, 1962) que lo mismo Virgilio que otros poetas latinos de su época se sirvieron deliberadamente de la sucesión de Fibonacci en sus composiciones.

En el reino vegetal, la sucesión de Fibonacci hace su aparición más llamativa en la implantación espiral de las semillas en ciertas variedades de girasol. Hay en ellas dos haces de espirales logarítmicas, una de sentido horario, otra en sentido antihorario. Los números de espirales son distintos en cada familia, y por lo común, números de Fibonacci consecutivos.

La lista de propiedades de la sucesión de Fibonacci bastaría para llenar un libro. Otro tanto puede decirse de sus aplicaciones en Física y Matemáticas. Leo Moser ha estudiado las trayectorias de rayos luminosos que inciden oblicuamente sobre dos láminas de vidrio planas y en contacto. Los rayos que no experimentan reflexión alguna atraviesan ambas láminas de sólo una forma; para los rayos que sufren una reflexión hay dos rutas posibles; cuando sufren dos reflexiones, las trayectorias son de tres tipos, y cuando sufren tres, de cinco. Al ir creciendo el número n de reflexiones, el número de trayectorias posibles va ajustándose a la sucesión de Fibonacci: para n reflexiones, el número de trayectorias es Fn+2. La sucesión puede utilizarse de forma parecida para contar el número de distintas rutas que puede seguir una abeja que va recorriendo las celdillas exagonales del panal; supondremos que la abeja se dirige siempre a una celdilla contigua y a la derecha de la que ocupa. Poco cuesta probar que hay sólo una ruta hasta la primera casilla, dos hasta la segunda, tres hasta la tercera, cinco itinerarios que conduzcan a la cuarta, y así sucesivamente. Al igual que antes, el número de trayectos es Fn+1, donde n es el número de casillas del problema. Y ya que viene a cuento, las abejas machos, o zánganos, no tienen padre. C. A. B. Smith ha hecho notar que cada zángano tiene madre, 2 abuelos (los padres de la madre), 3 bisabuelos (y no cuatro, pues el padre de la madre no tuvo padre), 5 tatarabuelos, y así sucesivamente, en sucesión de Fibonacci. David Klarner ha mostrado que los números de Fibonacci expresan de cuántas maneras podemos construir con dominós (rectángulos de tamaño 1 x 2) rectángulos de dimensión 2 x k. Hay sólo una manera de formar el rectángulo 2 x 1; 2 maneras de construir el cuadrado de 2 x 2; 3 para el rectángulo de 2 x 3; 5 para el de 2 x 4, y así sucesivamente.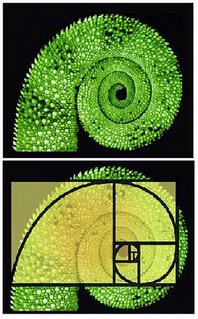

Cola de un camaleón

El más notable de los problemas abiertos concernientes a sucesiones de Fibonacci es el de si contienen o no colecciones infinitas de números primos. En una sucesión de Fibonacci generalizada, si los primeros números son divisibles ambos por un mismo número primo, todos los términos posteriores lo serán también, y es evidente que tales sucesiones no podrán contener más de un número primo. Supongamos, pues, que los dos primeros números sean primos entre sí (esto es, que su único común divisor sea 1). ¿Podrán existir sucesiones generalizadas que no contengan absolutamente ningún número primo? El primero en resolver esta cuestión fue R. L. Graham en A Fibonacci-like Sequence of Composite Numbers, en Mathematics Magazine, vol, 57, noviembre de 1964 pp. 322-24.

Fuente: Escuela Técnica Superior de Ingenierías Informática y de Telecomunicación